Analyst relations, Analyst, Datatec

علاقات المحلل: علاقات المحللين هي استراتيجية مؤسسية واتصالات مؤسسية ونشاط تسويقي تتواصل فيه الشركات مع محللي صناعة تكنولوجيا المعلومات والاتصالات الذين يعملون لصالح شركات بحثية واستشارية مستقلة مثل الشركات الأربع الرائدة.
المحلل: المحلل هو فرد يقوم بتحليل موضوع ما. قد يشير المصطلح إلى: محلل (مجلة) ، مجلة كيمياء محلل (برمجيات) ، برنامج قياس الطيف الكتلي محلل أعمال ، موظف يفحص احتياجات واهتمامات العملاء وأصحاب المصلحة محلل ألوان ، معلق رياضي يساعد المعلق الرئيسي محلل مالي ، وهو فرد يقوم بتحليل الأوراق المالية وحقوق الملكية التجارية في الاقتصاد والتمويل محلل خط اليد ، وهو الشخص الذي يقوم بتقييم الشخصية من خلال الكتابة اليدوية محلل الصناعة ، وهو الفرد الذي يقوم بأبحاث السوق على قطاعات الصناعات لتحديد الاتجاهات في الأعمال التجارية والتمويل محلل استخبارات محلل تسويق ، وهو الشخص الذي يقوم بتحليل بيانات السعر والعميل والمنافس والبيانات الاقتصادية لمساعدة الشركات محلل أخبار ، يفحص ويفسر بث الأخبار محلل عددي ، يطور ويحلل الخوارزميات العددية المحلل النفسي ، ممارس يعمل على تسهيل فهم عقل المريض اللاواعي محلل عام ، كيميائي مؤهل تعينه سلطة محلية في المملكة المتحدة محلل السياسة العامة ، وهو الفرد الذي يحلل تأثير السياسات العامة فيما يتعلق بأهدافها محلل كمي ، يطبق تقنيات رياضية على الخدمات المصرفية الاستثمارية ، وخاصة في مجالات إدارة المخاطر ، والتجارة ، والمشتقات المالية محلل أنظمة ، وهو فرد يقوم بتحليل التصميم الفني والتصميم الوظيفي لتطوير البرمجيات
داتاتيك: Datatec Limited ، المعروفة أيضًا باسم Datatec Group ، هي مجموعة خدمات متعددة الجنسيات لتكنولوجيا المعلومات والاتصالات (ICT) ومقرها جوهانسبرج ، جنوب إفريقيا. الأقسام الرئيسية للمجموعة هي: Westcon International ، dba Westcon-Comstor ، موزع التكنولوجيا ؛ Logicalis ، مزود خدمات مدارة لتكنولوجيا المعلومات ؛ والشركات Datatec Financial Services and Analysys Mason ، التي توفر التمويل ؛ وخدمات استشارات الاتصالات والإعلام والتكنولوجيا (TMT) ، على التوالي.
أناليتا: أناليتا هو جنس من العث من عائلة Crambidae.
أناليتا البيسيلاليس: Analyta albicillalis هي عثة في عائلة Crambidae. تم وصفه بواسطة Julius Lederer في عام 1863. تم العثور عليه في إندونيسيا وأستراليا ، حيث تم تسجيله في كوينزلاند.
أليتانا: Alytana هو جنس من العث من عائلة Crambidae. يحتوي على نوع واحد فقط ، Alytana aldabralis ، والذي يوجد في سيشيل ، حيث تم تسجيله من Aldabra و Assomption.
أناليتا أبيكاليس: Analyta apicalis هي عثة في عائلة Crambidae. وصفها جورج هامبسون في عام 1896. توجد في الهند وسريلانكا وتايوان.
أناليتا بوليانكورتي: Analyta beaulaincourti هي عثة في عائلة Crambidae . تم وصفه من قبل Rougeot في عام 1977. تم العثور عليه في جيبوتي.
أناليتا كاليجراماليس: Analyta calligrammalis هو نوع من العثة من عائلة Crambidae. توجد في سيراليون وغانا ومدغشقر وسيشيل وكذلك في الكاميرون وغامبيا ونيجيريا وجنوب إفريقيا ومالي.
أناليتا جاماليس: Analyta gammalis هو نوع من العثة من عائلة Crambidae. وصفه بيير فييت في عام 1958 وهو موجود في شرق مدغشقر.
أناليتا هيرانيسياليس: Analyta heranicealis هي عثة في عائلة Crambidae . وصفها فرانسيس والكر عام 1859. تم العثور عليها في بورنيو.
أناليتا نيجريفلافاليس: Analyta nigriflavalis هي عثة في عائلة Crambidae . وصفه جورج هامبسون في عام 1913. تم العثور عليه في نيجيريا.
أناليتا بيرفينكا: Analyta pervinca هي عثة في عائلة Crambidae . وصفه جان جيسكيير في عام 1942. تم العثور عليه في جمهورية الكونغو الديمقراطية ، حيث تم تسجيله من مقاطعة كاتانغا.
أناليتا أبيكاليس: Analyta apicalis هي عثة في عائلة Crambidae. وصفها جورج هامبسون في عام 1896. توجد في الهند وسريلانكا وتايوان.
أناليتا سيمانتريس: Analyta semantris هي عثة في عائلة Crambidae . وصفه هاريسون جراي ديار جونيور في عام 1914. تم العثور عليه في بنما وغيانا الفرنسية.
أناليتا فانسوميريني: Analyta vansomereni هي عثة في عائلة Crambidae . تم وصفه من قبل تامس في عام 1932. تم العثور عليه في كينيا.
أناليتارشا: Analytarcha هو جنس من العث ينتمي إلى عائلة Tineidae.
المحللة: المادة التحليلية أو المكونة أو الأنواع الكيميائية هي مادة أو مكون كيميائي مهم في إجراء تحليلي. يشار إلى أنقى المواد بالتحليل. مثال: ذهب عيار 24 ، كلوريد الصوديوم ، ماء ، إلخ. في الواقع ، لم يتم العثور على أي مادة نقية بنسبة 100٪ في جودتها ، لذلك نطلق على المادة التي تم العثور عليها على أنها أكثر نقاءًا.
كاشف خاص بالتحليل: الكواشف الخاصة بالتحليل ( ASR s) هي فئة من الجزيئات البيولوجية التي يمكن استخدامها لتحديد وقياس كمية مادة كيميائية فردية في العينات البيولوجية.
كاشف خاص بالتحليل: الكواشف الخاصة بالتحليل ( ASR s) هي فئة من الجزيئات البيولوجية التي يمكن استخدامها لتحديد وقياس كمية مادة كيميائية فردية في العينات البيولوجية.
كاشف خاص بالتحليل: الكواشف الخاصة بالتحليل ( ASR s) هي فئة من الجزيئات البيولوجية التي يمكن استخدامها لتحديد وقياس كمية مادة كيميائية فردية في العينات البيولوجية.
المحللة: المادة التحليلية أو المكونة أو الأنواع الكيميائية هي مادة أو مكون كيميائي مهم في إجراء تحليلي. يشار إلى أنقى المواد بالتحليل. مثال: ذهب عيار 24 ، كلوريد الصوديوم ، ماء ، إلخ. في الواقع ، لم يتم العثور على أي مادة نقية بنسبة 100٪ في جودتها ، لذلك نطلق على المادة التي تم العثور عليها على أنها أكثر نقاءًا.
تحليلي: بصفة عامة ، يشير مصطلح " التحليلي " إلى "القدرة على التحليل" أو "التقسيم إلى عناصر أو مبادئ".
التمييز التحليلي التركيبي: التمييز التحليلي التركيبي هو تمييز دلالي ، يستخدم بشكل أساسي في الفلسفة للتمييز بين الافتراضات التي تتكون من نوعين: الافتراضات التحليلية والافتراضات التركيبية . تكون الافتراضات التحليلية صحيحة أو غير صحيحة فقط بحكم معناها ، في حين أن حقيقة الافتراضات التركيبية ، إن وجدت ، مشتقة من كيفية ارتباط معناها بالعالم.
التمييز التحليلي التركيبي: التمييز التحليلي التركيبي هو تمييز دلالي ، يستخدم بشكل أساسي في الفلسفة للتمييز بين الافتراضات التي تتكون من نوعين: الافتراضات التحليلية والافتراضات التركيبية . تكون الافتراضات التحليلية صحيحة أو غير صحيحة فقط بحكم معناها ، في حين أن حقيقة الافتراضات التركيبية ، إن وجدت ، مشتقة من كيفية ارتباط معناها بالعالم.
تحليلي: بصفة عامة ، يشير مصطلح " التحليلي " إلى "القدرة على التحليل" أو "التقسيم إلى عناصر أو مبادئ".
لغة تحليلية: في التصنيف اللغوي ، اللغة التحليلية هي لغة تنقل العلاقات بين الكلمات في الجمل بشكل أساسي عن طريق الكلمات المساعدة وترتيب الكلمات ، بدلاً من استخدام التصريفات. على سبيل المثال ، العبارة الإنجليزية "القطة تطارد الكرة" تنقل حقيقة أن القطة تعمل على الكرة بشكل تحليلي عبر ترتيب الكلمات. يمكن أن يتناقض هذا مع اللغات التركيبية ، التي تعتمد بشكل كبير على التصريفات لنقل العلاقات بين الكلمات. معظم اللغات ليست تحليلية بحتة ، لكن العديد منها يعتمد بشكل أساسي على التركيب التحليلي.
تطبيقات تحليلية: التطبيقات التحليلية هي نوع من برامج تطبيقات الأعمال ، تُستخدم لقياس وتحسين أداء العمليات التجارية. وبشكل أكثر تحديدًا ، تعد التطبيقات التحليلية نوعًا من ذكاء الأعمال. على هذا النحو ، يستخدمون مجموعات من البيانات التاريخية حول العمليات التجارية لتزويد مستخدمي الأعمال بالمعلومات والأدوات التي تسمح لهم بإجراء تحسينات في وظائف الأعمال.
التوليفات التحليلية: التوليفات التحليلية هو كتاب عن رياضيات التعداد التجميعي ، باستخدام وظائف التوليد والتحليل المعقد لفهم معدلات نمو أعداد الكائنات التوافقية. كتبه فيليب فلاجوليه وروبرت سيدجويك ، ونشرته مطبعة جامعة كامبريدج في عام 2009. وفاز بجائزة ليروي بي ستيل في عام 2019.
التكعيبية: التكعيبية هي حركة فنية طليعية من أوائل القرن العشرين أحدثت ثورة في الرسم والنحت الأوروبي ، وألهمت الحركات ذات الصلة في الموسيقى والأدب والهندسة المعمارية. في العمل الفني التكعيبي ، يتم تحليل الكائنات وتقسيمها وإعادة تجميعها في شكل مجردة - بدلاً من تصوير الكائنات من وجهة نظر واحدة ، يصور الفنان الموضوع من عدة وجهات نظر لتمثيل الموضوع في سياق أكبر. تعتبر التكعيبية من أكثر الحركات الفنية تأثيراً في القرن العشرين. يستخدم المصطلح على نطاق واسع بالاقتران مع مجموعة واسعة من الأعمال الفنية المنتجة في باريس أو بالقرب من باريس (بوتو) خلال العقد الأول من القرن العشرين وخلال عشرينيات القرن الماضي.
طريقة العنصر التحليلي: طريقة العنصر التحليلي ( AEM ) هي طريقة عددية تستخدم لحل المعادلات التفاضلية الجزئية. تم تطويره في البداية بواسطة ODL Strack في جامعة مينيسوتا. وهي مشابهة بطبيعتها لطريقة العناصر الحدودية (BEM) ، لأنها لا تعتمد على تقدير الأحجام أو المناطق في النظام النموذجي ؛ يتم تحديد الحدود الداخلية والخارجية فقط. أحد الفروق الأساسية بين AEM و BEM هو أنه يتم حساب تكاملات الحدود بشكل تحليلي.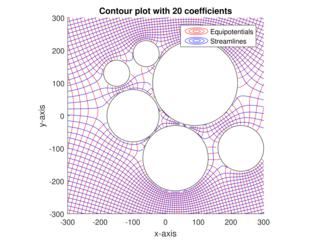
المحرك التحليلي: كان المحرك التحليلي عبارة عن كمبيوتر ميكانيكي متعدد الأغراض مقترح صممه عالم الرياضيات الإنجليزي ورائد الكمبيوتر تشارلز باباج. تم وصفه لأول مرة في عام 1837 على أنه خليفة محرك الفرق الخاص باباج ، والذي كان تصميمًا لجهاز كمبيوتر ميكانيكي أبسط.
نظرية فريدهولم التحليلية: في الرياضيات ، نظرية فريدهولم التحليلية هي نتيجة تتعلق بوجود انعكاسات محدودة لعائلة من المشغلين الخطيين المحدودين على فضاء هيلبرت. إنه أساس نظريتين كلاسيكيتين وهامتين ، بديل فريدهولم ونظرية هيلبرت شميت. تمت تسمية النتيجة على اسم عالم الرياضيات السويدي إريك إيفار فريدهولم.
الهندسة التحليلية: في الرياضيات الكلاسيكية ، الهندسة التحليلية ، والمعروفة أيضًا باسم هندسة الإحداثيات أو الهندسة الديكارتية ، هي دراسة الهندسة باستخدام نظام إحداثيات. هذا يتناقض مع الهندسة التركيبية.
ويلفريد سيلارز: كان ويلفريد ستوكر سيلارز فيلسوفًا أمريكيًا ومطورًا بارزًا للواقعية النقدية ، والذي "أحدث ثورة في كل من المحتوى ومنهج الفلسفة في الولايات المتحدة".
عملية التحليل الوراثي: عملية التسلسل الهرمي التحليلي ( AHP ) ، وهي أيضًا عملية التسلسل الهرمي التحليلي ، هي تقنية منظمة لتنظيم وتحليل القرارات المعقدة ، بناءً على الرياضيات وعلم النفس. تم تطويره بواسطة Thomas L. Saaty في السبعينيات ؛ دخلت Saaty في شراكة مع Ernest Forman لتطوير برنامج Expert Choice في عام 1983 ، وخضع برنامج AHP للدراسة والتنقيح على نطاق واسع منذ ذلك الحين. إنه يمثل نهجًا دقيقًا لتحديد أوزان معايير القرار. تُستخدم خبرات الخبراء الفرديين لتقدير المقادير النسبية للعوامل من خلال المقارنات الزوجية. يقارن كل من المستجيبين الأهمية النسبية لكل زوج من العناصر باستخدام استبيان مصمم خصيصًا.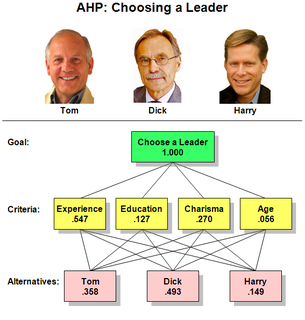
الفقه التحليلي: الفقه التحليلي هو نهج فلسفي للقانون يعتمد على موارد الفلسفة التحليلية الحديثة لمحاولة فهم طبيعتها. نظرًا لأن حدود الفلسفة التحليلية غامضة نوعًا ما ، فمن الصعب تحديد مدى امتدادها. ربما كان HLA Hart هو الكاتب الأكثر تأثيراً في مدرسة الفقه التحليلي الحديثة ، على الرغم من أن تاريخها يعود على الأقل إلى جيريمي بينثام.
الوظيفة التحليلية: في الرياضيات ، الوظيفة التحليلية هي وظيفة تُعطى محليًا بواسطة سلسلة قوى متقاربة. توجد وظائف تحليلية حقيقية ووظائف تحليلية معقدة . وظائف كل نوع قابلة للتفاضل إلى ما لا نهاية ، ولكن الوظائف التحليلية المعقدة تظهر خصائص لا تنطبق بشكل عام على الوظائف التحليلية الحقيقية. تكون الوظيفة تحليلية فقط إذا كانت سلسلة Taylor الخاصة بها حول x 0 تتقارب مع الوظيفة في بعض الجوار لكل x 0 في مجالها.
الماركسية التحليلية: الماركسية التحليلية هي مقاربة للنظرية الماركسية كانت بارزة بين الفلاسفة المتحدثين بالإنجليزية وعلماء الاجتماع خلال الثمانينيات. كان مرتبطًا بشكل أساسي بمجموعة سبتمبر من الأكاديميين ، والتي سميت بذلك بسبب اجتماعات سبتمبر التي تعقد كل سنتين لمناقشة الاهتمامات المشتركة. كوهين ، التي وصفها ج. أ. كوهين ، بأنها "ماركسية غير هراء" ، تميزت ، على حد تعبير ديفيد ميللر ، بـ "تفكير واضح وصارم حول الأسئلة التي عادة ما يغطيها الضباب الأيديولوجي. يسعى أعضاء هذه المدرسة إلى تطبيق تقنيات الفلسفة التحليلية ، إلى جانب أدوات العلوم الاجتماعية الحديثة مثل نظرية الاختيار العقلاني ، لتوضيح نظريات كارل ماركس وخلفائه.
عملية الشبكة التحليلية: عملية الشبكة التحليلية ( ANP ) هي شكل أكثر عمومية لعملية التسلسل الهرمي التحليلي (AHP) المستخدمة في تحليل القرار متعدد المعايير.
نظرية الأعداد التحليلية: في الرياضيات ، تعتبر نظرية الأعداد التحليلية فرعًا من فروع نظرية الأعداد التي تستخدم طرقًا من التحليل الرياضي لحل المشكلات المتعلقة بالأعداد الصحيحة. غالبًا ما يقال أنها بدأت مع مقدمة بيتر جوستاف ليجون ديريتشليت عام 1837 لوظائف Dirichlet L لإعطاء أول دليل على نظرية ديريتشليت في التقدم الحسابي. وهي معروفة بنتائجها على الأعداد الأولية ونظرية الأعداد المضافة.
الفلسفة التحليلية: الفلسفة التحليلية هي فرع من فروع وتقليد الفلسفة باستخدام التحليل الذي يحظى بشعبية في العالم الغربي وخاصة المحيط الإنجليزي ، والذي بدأ في مطلع القرن العشرين في العصر المعاصر ويستمر حتى يومنا هذا. في المملكة المتحدة والولايات المتحدة وكندا وأستراليا ونيوزيلندا والدول الاسكندنافية ، تعرّف غالبية أقسام الفلسفة الجامعية اليوم نفسها على أنها أقسام "تحليلية".
الفلسفة التحليلية: الفلسفة التحليلية هي فرع من فروع وتقليد الفلسفة باستخدام التحليل الذي يحظى بشعبية في العالم الغربي وخاصة المحيط الإنجليزي ، والذي بدأ في مطلع القرن العشرين في العصر المعاصر ويستمر حتى يومنا هذا. في المملكة المتحدة والولايات المتحدة وكندا وأستراليا ونيوزيلندا والدول الاسكندنافية ، تعرّف غالبية أقسام الفلسفة الجامعية اليوم نفسها على أنها أقسام "تحليلية".
الفلسفة التحليلية (مجلة): الفلسفة التحليلية هي مجلة أكاديمية فصلية تخضع لمراجعة الأقران وتغطي جميع مجالات الفلسفة. تم نشره من قبل وايلي ورئيس التحرير ديفيد سوسا. تأسست في عام 1960 باسم كتب فلسفية ، وحصلت على لقبها الحالي في عام 2011.
الصوتيات التحليلية: تشير الأصوات التحليلية إلى نهج شائع جدًا لتدريس القراءة يبدأ على مستوى الكلمة ، وليس على مستوى الصوت (الصوت). إنه لا يعلم مزج الأصوات معًا كما هو الحال في الصوتيات الاصطناعية. تتمثل إحدى الطرق في جعل الطلاب يتعرفون على صوت مشترك في مجموعة من الكلمات تحتوي كل منها على نفس الصوت. على سبيل المثال ، يناقش المعلم والطالب كيف تتشابه الكلمات التالية: بات ، بارك ، ادفع وقلم . غالبًا ما يتم تدريس الصوتيات التحليلية جنبًا إلى جنب مع كتب القراءة المتساوية ، وممارسة النظرة ، واستخدام الوسائل المساعدة مثل أوراق عمل الصوتيات.
تايلور وفرانسيس: مجموعة Taylor & Francis هي شركة دولية نشأت في إنجلترا وتنشر الكتب والمجلات الأكاديمية. وهي قسم من Informa plc ، وهي شركة ناشر ومؤتمرات مقرها المملكة المتحدة.
التمييز التحليلي التركيبي: التمييز التحليلي التركيبي هو تمييز دلالي ، يستخدم بشكل أساسي في الفلسفة للتمييز بين الافتراضات التي تتكون من نوعين: الافتراضات التحليلية والافتراضات التركيبية . تكون الافتراضات التحليلية صحيحة أو غير صحيحة فقط بحكم معناها ، في حين أن حقيقة الافتراضات التركيبية ، إن وجدت ، مشتقة من كيفية ارتباط معناها بالعالم.
علم النفس التحليلي: علم النفس التحليلي هو مصطلح صاغه الطبيب النفسي السويسري كارل يونج ، لوصف البحث في "علمه التجريبي الجديد" للنفسية. وقد صمم هذا البرنامج لتمييزه عن نظريات التحليل النفسي فرويد كما تعاونهما سبع سنوات على التحليل النفسي كان يقترب من نهايته بين 1912 و 1913. ويرد تطور العلم في بلده التأليف ضخمة، والأشغال التي يتم جمعها، وكتب أكثر من ستين عاما من حياته وقت الحياة.
إشارة تحليلية: في الرياضيات ومعالجة الإشارات ، تعد الإشارة التحليلية دالة ذات قيمة معقدة لا تحتوي على مكونات تردد سالبة. الأجزاء الحقيقية والخيالية للإشارة التحليلية هي وظائف ذات قيمة حقيقية مرتبطة ببعضها البعض بواسطة تحويل هيلبرت.
الفلسفة التحليلية: الفلسفة التحليلية هي فرع من فروع وتقليد الفلسفة باستخدام التحليل الذي يحظى بشعبية في العالم الغربي وخاصة المحيط الإنجليزي ، والذي بدأ في مطلع القرن العشرين في العصر المعاصر ويستمر حتى يومنا هذا. في المملكة المتحدة والولايات المتحدة وكندا وأستراليا ونيوزيلندا والدول الاسكندنافية ، تعرّف غالبية أقسام الفلسفة الجامعية اليوم نفسها على أنها أقسام "تحليلية".
الدراسات الإحصائية التحليلية والعددية: الدراسات الإحصائية التحليلية والتعدادية نوعان من الدراسات العلمية:
التمييز التحليلي التركيبي: التمييز التحليلي التركيبي هو تمييز دلالي ، يستخدم بشكل أساسي في الفلسفة للتمييز بين الافتراضات التي تتكون من نوعين: الافتراضات التحليلية والافتراضات التركيبية . تكون الافتراضات التحليلية صحيحة أو غير صحيحة فقط بحكم معناها ، في حين أن حقيقة الافتراضات التركيبية ، إن وجدت ، مشتقة من كيفية ارتباط معناها بالعالم.
التمييز التحليلي التركيبي: التمييز التحليلي التركيبي هو تمييز دلالي ، يستخدم بشكل أساسي في الفلسفة للتمييز بين الافتراضات التي تتكون من نوعين: الافتراضات التحليلية والافتراضات التركيبية . تكون الافتراضات التحليلية صحيحة أو غير صحيحة فقط بحكم معناها ، في حين أن حقيقة الافتراضات التركيبية ، إن وجدت ، مشتقة من كيفية ارتباط معناها بالعالم.
التمييز التحليلي التركيبي: التمييز التحليلي التركيبي هو تمييز دلالي ، يستخدم بشكل أساسي في الفلسفة للتمييز بين الافتراضات التي تتكون من نوعين: الافتراضات التحليلية والافتراضات التركيبية . تكون الافتراضات التحليلية صحيحة أو غير صحيحة فقط بحكم معناها ، في حين أن حقيقة الافتراضات التركيبية ، إن وجدت ، مشتقة من كيفية ارتباط معناها بالعالم.
تطبيقات تحليلية: التطبيقات التحليلية هي نوع من برامج تطبيقات الأعمال ، تُستخدم لقياس وتحسين أداء العمليات التجارية. وبشكل أكثر تحديدًا ، تعد التطبيقات التحليلية نوعًا من ذكاء الأعمال. على هذا النحو ، يستخدمون مجموعات من البيانات التاريخية حول العمليات التجارية لتزويد مستخدمي الأعمال بالمعلومات والأدوات التي تسمح لهم بإجراء تحسينات في وظائف الأعمال.
apriori التحليلي: قد يشير apriori التحليلي إلى: بداهة وبعدية التمييز التحليلي التركيبي الحقيقة التحليلية
فهرس: الببليوغرافيا ، كنظام دراسي ، هي تقليديًا الدراسة الأكاديمية للكتب كأشياء مادية وثقافية ؛ بهذا المعنى ، يُعرف أيضًا باسم علم المراجع . يصف المؤلف والببليوغرافيا الإنجليزي جون كارتر الببليوغرافيا بأنها كلمة لها معنون ، أحدهما ، قائمة بالكتب لمزيد من الدراسة أو للأعمال التي استشارها المؤلف ؛ والآخر ، الذي ينطبق على الجامعين ، هو "دراسة الكتب كأشياء مادية" و "الوصف المنهجي للكتب كأشياء".
القدرة التحليلية: في الانضباط الرياضي للتحليل المعقد ، فإن القدرة التحليلية لمجموعة فرعية مدمجة K للمستوى المعقد هي رقم يشير إلى "حجم" دالة تحليلية محدودة على C \\ K يمكن أن تصبح. بشكل تقريبي ، تقيس γ ( K ) حجم كرة الوحدة لمساحة الوظائف التحليلية المحدودة خارج K.
الكيمياء التحليلية: دراسات الكيمياء التحليلية واستخدام الأدوات والطرق المستخدمة لفصل وتحديد وقياس المادة. في الممارسة العملية ، قد يشكل الفصل أو التحديد أو التحديد الكمي التحليل بأكمله أو يتم دمجه مع طريقة أخرى. الفصل يعزل المواد التحليلية. يحدد التحليل النوعي التحليلات ، بينما يحدد التحليل الكمي الكمية العددية أو التركيز.
صيغة رقم الفصل: في نظرية الأعداد ، تربط صيغة رقم الصنف العديد من الثوابت المهمة لحقل رقم بقيمة خاصة لوظيفة زيتا Dedekind.
الطريقة الرمزية (التوافقية): في التوافقية ، الطريقة الرمزية هي تقنية لحساب الكائنات التوافقية. يستخدم الهيكل الداخلي للكائنات لاشتقاق الصيغ لوظائف التوليد الخاصة بهم. ترتبط الطريقة في الغالب بفيليب فلاجوليت وتم تفصيلها في الجزء الأول من كتابه مع روبرت سيدجويك ، التوليفات التحليلية ، بينما يشرح باقي الكتاب كيفية استخدام التحليل المعقد من أجل الحصول على نتائج مقاربة واحتمالية على وظائف التوليد المقابلة.
الثقة التحليلية: الثقة التحليلية هي تصنيف يستخدمه محللو الاستخبارات لنقل الشك إلى صانعي القرار حول بيان الاحتمال التقديري. تنشأ الحاجة إلى تقييمات الثقة التحليلية من معرفة المحللين غير الكاملة للنموذج المفاهيمي. أزواج تصنيف ثقة تحليلي مع بيان باستخدام كلمة الاحتمال التقديري لتشكيل بيان تحليلي كامل. الأساليب العلمية لتحديد الثقة التحليلية لا تزال في مرحلة الطفولة.
الاستمرار التحليلي: في التحليل المعقد ، وهو فرع من فروع الرياضيات ، تعتبر الاستمرارية التحليلية تقنية لتوسيع مجال تعريف وظيفة تحليلية معينة. غالبًا ما تنجح الاستمرار التحليلية في تحديد قيم إضافية لوظيفة ما ، على سبيل المثال في منطقة جديدة حيث يصبح تمثيل السلاسل اللانهائية من حيث تعريفها في البداية متشعبًا.
الاستمرار التحليلي العددي: في فيزياء الأجسام المتعددة ، تكمن مشكلة الاستمرار التحليلي في الاستخراج العددي للكثافة الطيفية لوظيفة خضراء نظرًا لقيمها على المحور التخيلي. إنها خطوة معالجة لاحقة ضرورية لحساب الخصائص الديناميكية للأنظمة الفيزيائية من محاكاة مونت كارلو الكمومية ، والتي غالبًا ما تحسب قيم الوظيفة الخضراء فقط في الأوقات التخيلية أو ترددات ماتسوبارا.
نظرية أحادية اللون: في التحليل المعقد ، تعتبر نظرية أحادية اللون نتيجة مهمة حول الاستمرار التحليلي لوظيفة تحليلية معقدة لمجموعة أكبر. الفكرة هي أنه يمكن للمرء أن يوسع دالة تحليلية معقدة على طول منحنيات تبدأ في المجال الأصلي للوظيفة وتنتهي في المجموعة الأكبر. من المشاكل المحتملة لهذا الاستمرارية التحليلية على طول إستراتيجية المنحنى وجود العديد من المنحنيات التي تنتهي عند نفس النقطة في المجموعة الأكبر. تعطي نظرية أحادية اللون شروطًا كافية للاستمرار التحليلي لإعطاء نفس القيمة عند نقطة معينة بغض النظر عن المنحنى المستخدم للوصول إلى هناك ، بحيث تكون الوظيفة التحليلية الممتدة الناتجة محددة جيدًا وذات قيمة واحدة.
الاستمرار التحليلي: في التحليل المعقد ، وهو فرع من فروع الرياضيات ، تعتبر الاستمرارية التحليلية تقنية لتوسيع مجال تعريف وظيفة تحليلية معينة. غالبًا ما تنجح الاستمرار التحليلية في تحديد قيم إضافية لوظيفة ما ، على سبيل المثال في منطقة جديدة حيث يصبح تمثيل السلاسل اللانهائية من حيث تعريفها في البداية متشعبًا.
الاستمرار التحليلي: في التحليل المعقد ، وهو فرع من فروع الرياضيات ، تعتبر الاستمرارية التحليلية تقنية لتوسيع مجال تعريف وظيفة تحليلية معينة. غالبًا ما تنجح الاستمرار التحليلية في تحديد قيم إضافية لوظيفة ما ، على سبيل المثال في منطقة جديدة حيث يصبح تمثيل السلاسل اللانهائية من حيث تعريفها في البداية متشعبًا.
التكعيبية: التكعيبية هي حركة فنية طليعية من أوائل القرن العشرين أحدثت ثورة في الرسم والنحت الأوروبي ، وألهمت الحركات ذات الصلة في الموسيقى والأدب والهندسة المعمارية. في العمل الفني التكعيبي ، يتم تحليل الكائنات وتقسيمها وإعادة تجميعها في شكل مجردة - بدلاً من تصوير الكائنات من وجهة نظر واحدة ، يصور الفنان الموضوع من عدة وجهات نظر لتمثيل الموضوع في سياق أكبر. تعتبر التكعيبية من أكثر الحركات الفنية تأثيراً في القرن العشرين. يستخدم المصطلح على نطاق واسع بالاقتران مع مجموعة واسعة من الأعمال الفنية المنتجة في باريس أو بالقرب من باريس (بوتو) خلال العقد الأول من القرن العشرين وخلال عشرينيات القرن الماضي.
الوظيفة التحليلية: في الرياضيات ، الوظيفة التحليلية هي وظيفة تُعطى محليًا بواسطة سلسلة قوى متقاربة. توجد وظائف تحليلية حقيقية ووظائف تحليلية معقدة . وظائف كل نوع قابلة للتفاضل إلى ما لا نهاية ، ولكن الوظائف التحليلية المعقدة تظهر خصائص لا تنطبق بشكل عام على الوظائف التحليلية الحقيقية. تكون الوظيفة تحليلية فقط إذا كانت سلسلة Taylor الخاصة بها حول x 0 تتقارب مع الوظيفة في بعض الجوار لكل x 0 في مجالها.
الدورة الجبرية: في الرياضيات ، الدورة الجبرية على صنف جبري V عبارة عن تركيبة خطية رسمية من الأنواع الفرعية لـ V. هذا هو جزء من الطوبولوجيا الجبرية لـ V التي يمكن الوصول إليها مباشرة بالطرق الجبرية. إن فهم الدورات الجبرية على مجموعة متنوعة يمكن أن يعطي رؤى عميقة في بنية الصنف.
كثافة ديريتشليت: في الرياضيات ، تعد كثافة Dirichlet لمجموعة من الأعداد الأولية ، التي سميت باسم Peter Gustav Lejeune Dirichlet ، مقياسًا لحجم المجموعة التي يسهل استخدامها من الكثافة الطبيعية.
الفلسفة التحليلية: الفلسفة التحليلية هي فرع من فروع وتقليد الفلسفة باستخدام التحليل الذي يحظى بشعبية في العالم الغربي وخاصة المحيط الإنجليزي ، والذي بدأ في مطلع القرن العشرين في العصر المعاصر ويستمر حتى يومنا هذا. في المملكة المتحدة والولايات المتحدة وكندا وأستراليا ونيوزيلندا والدول الاسكندنافية ، تعرّف غالبية أقسام الفلسفة الجامعية اليوم نفسها على أنها أقسام "تحليلية".
التشريح التحليلي: التشريح التحليلي هو مفهوم في تحليل قانون حقوق التأليف والنشر الأمريكي لبرامج الكمبيوتر. التشريح التحليلي هو أداة لتحديد ما إذا كان العمل المتهم بانتهاك حقوق الطبع والنشر مشابهًا إلى حد كبير للعمل المحمي بحقوق الطبع والنشر.
طريقة العنصر التحليلي: طريقة العنصر التحليلي ( AEM ) هي طريقة عددية تستخدم لحل المعادلات التفاضلية الجزئية. تم تطويره في البداية بواسطة ODL Strack في جامعة مينيسوتا. وهي مشابهة بطبيعتها لطريقة العناصر الحدودية (BEM) ، لأنها لا تعتمد على تقدير الأحجام أو المناطق في النظام النموذجي ؛ يتم تحديد الحدود الداخلية والخارجية فقط. أحد الفروق الأساسية بين AEM و BEM هو أنه يتم حساب تكاملات الحدود بشكل تحليلي.
المحرك التحليلي: كان المحرك التحليلي عبارة عن كمبيوتر ميكانيكي متعدد الأغراض مقترح صممه عالم الرياضيات الإنجليزي ورائد الكمبيوتر تشارلز باباج. تم وصفه لأول مرة في عام 1837 على أنه خليفة محرك الفرق الخاص باباج ، والذي كان تصميمًا لجهاز كمبيوتر ميكانيكي أبسط.
ما وراء الأخلاق: في الميتافيلوسوفا والأخلاق ، ما وراء الأخلاق هي دراسة طبيعة ونطاق ومعنى الحكم الأخلاقي. إنه أحد الفروع الثلاثة للأخلاق التي درسها الفلاسفة بشكل عام ، والفروع الأخرى هي الأخلاق المعيارية والأخلاق التطبيقية.
تعبير مغلق الشكل: في الرياضيات ، التعبير ذو الشكل المغلق هو تعبير رياضي يتم التعبير عنه باستخدام عدد محدود من العمليات القياسية. قد يحتوي على ثوابت ، ومتغيرات ، وعمليات ووظائف "معروفة" ، ولكن عادة لا يوجد حد ، أو تفاضل ، أو تكامل. قد تختلف مجموعة العمليات والوظائف المقبولة في التعبير ذي الشكل المغلق باختلاف المؤلف والسياق.
الاستمرار التحليلي: في التحليل المعقد ، وهو فرع من فروع الرياضيات ، تعتبر الاستمرارية التحليلية تقنية لتوسيع مجال تعريف وظيفة تحليلية معينة. غالبًا ما تنجح الاستمرار التحليلية في تحديد قيم إضافية لوظيفة ما ، على سبيل المثال في منطقة جديدة حيث يصبح تمثيل السلاسل اللانهائية من حيث تعريفها في البداية متشعبًا.
النسوية التحليلية: النسوية التحليلية هي خط فلسفي يطبق المفاهيم والأساليب التحليلية على القضايا النسوية ويطبق المفاهيم والرؤى النسوية على القضايا التي كانت تقليديا محل اهتمام الفلاسفة التحليليين. مثل جميع النسويات ، تصر النسويات التحليلية على الاعتراف والتمييز على أساس الجنس والفلسفة الذكرية والطعن فيهما.
تعبير مغلق الشكل: في الرياضيات ، التعبير ذو الشكل المغلق هو تعبير رياضي يتم التعبير عنه باستخدام عدد محدود من العمليات القياسية. قد يحتوي على ثوابت ، ومتغيرات ، وعمليات ووظائف "معروفة" ، ولكن عادة لا يوجد حد ، أو تفاضل ، أو تكامل. قد تختلف مجموعة العمليات والوظائف المقبولة في التعبير ذي الشكل المغلق باختلاف المؤلف والسياق.
تعبير مغلق الشكل: في الرياضيات ، التعبير ذو الشكل المغلق هو تعبير رياضي يتم التعبير عنه باستخدام عدد محدود من العمليات القياسية. قد يحتوي على ثوابت ، ومتغيرات ، وعمليات ووظائف "معروفة" ، ولكن عادة لا يوجد حد ، أو تفاضل ، أو تكامل. قد تختلف مجموعة العمليات والوظائف المقبولة في التعبير ذي الشكل المغلق باختلاف المؤلف والسياق.
الإطار التحليلي: الإطار التحليلي هو رسم تفصيلي أو مخطط تفصيلي لبعض الظواهر الاجتماعية ، ويمثل الفكرة الأولية لعالم يحلل هذه الظاهرة. يُعرِّفها Charles C. معظم الظواهر التي تم تحليلها.
الإطار التحليلي: الإطار التحليلي هو رسم تفصيلي أو مخطط تفصيلي لبعض الظواهر الاجتماعية ، ويمثل الفكرة الأولية لعالم يحلل هذه الظاهرة. يُعرِّفها Charles C. معظم الظواهر التي تم تحليلها.
نظرية فريدهولم التحليلية: في الرياضيات ، نظرية فريدهولم التحليلية هي نتيجة تتعلق بوجود انعكاسات محدودة لعائلة من المشغلين الخطيين المحدودين على فضاء هيلبرت. إنه أساس نظريتين كلاسيكيتين وهامتين ، بديل فريدهولم ونظرية هيلبرت شميت. تمت تسمية النتيجة على اسم عالم الرياضيات السويدي إريك إيفار فريدهولم.
الوظيفة التحليلية: في الرياضيات ، الوظيفة التحليلية هي وظيفة تُعطى محليًا بواسطة سلسلة قوى متقاربة. توجد وظائف تحليلية حقيقية ووظائف تحليلية معقدة . وظائف كل نوع قابلة للتفاضل إلى ما لا نهاية ، ولكن الوظائف التحليلية المعقدة تظهر خصائص لا تنطبق بشكل عام على الوظائف التحليلية الحقيقية. تكون الوظيفة تحليلية فقط إذا كانت سلسلة Taylor الخاصة بها حول x 0 تتقارب مع الوظيفة في بعض الجوار لكل x 0 في مجالها.
وظيفة النافذة (SQL): في SQL ، وظيفة النافذة أو الوظيفة التحليلية هي وظيفة تستخدم قيمًا من صف واحد أو عدة صفوف لإرجاع قيمة لكل صف. تحتوي وظائف النافذة على عبارة OVER ؛ أي وظيفة بدون جملة OVER ليست وظيفة نافذة ، بل هي دالة مجمعة أو صف واحد (سلمي).
الوظيفة التحليلية للمصفوفة: في الرياضيات ، يمكن استخدام كل دالة تحليلية لتعريف دالة مصفوفة تقوم بتعيين المصفوفات المربعة ذات الإدخالات المعقدة إلى المصفوفات المربعة من نفس الحجم.
الهولومورفي اللانهائي الأبعاد: في الرياضيات ، تعد الأشكال اللانهائية ذات الأبعاد اللانهائية فرعًا من التحليل الوظيفي. يهتم بتعميمات مفهوم الوظيفة الشاملة للوظائف المحددة واتخاذ القيم في فضاءات باناخ المعقدة ، عادةً ذات البعد اللانهائي. إنه أحد جوانب التحليل الوظيفي غير الخطي.
الوظيفية (فلسفة العقل): في فلسفة العقل ، الوظيفية هي أطروحة أن الحالات العقلية تتشكل فقط من خلال دورها الوظيفي ، مما يعني ، علاقاتها السببية مع الحالات العقلية الأخرى ، والمدخلات الحسية والمخرجات السلوكية. تطورت الوظيفية إلى حد كبير كبديل لنظرية هوية العقل والسلوكية.
الوظيفة التحليلية: في الرياضيات ، الوظيفة التحليلية هي وظيفة تُعطى محليًا بواسطة سلسلة قوى متقاربة. توجد وظائف تحليلية حقيقية ووظائف تحليلية معقدة . وظائف كل نوع قابلة للتفاضل إلى ما لا نهاية ، ولكن الوظائف التحليلية المعقدة تظهر خصائص لا تنطبق بشكل عام على الوظائف التحليلية الحقيقية. تكون الوظيفة تحليلية فقط إذا كانت سلسلة Taylor الخاصة بها حول x 0 تتقارب مع الوظيفة في بعض الجوار لكل x 0 في مجالها.
حساب المنفذين: في الطوبولوجيا الجبرية ، وهي فرع من فروع الرياضيات ، أو حساب المنفذين أو حساب Goodwillie هو أسلوب لدراسة المفاعلات عن طريق تقريبها من خلال سلسلة من الدوال الأبسط ؛ فإنه يعمم sheafification من presheaf. هذا التسلسل التقريبي يشبه بشكل رسمي سلسلة تايلور للدالة السلسة ، ومن هنا جاء مصطلح " حساب التفاضل والتكامل ".
الهندسة التحليلية: في الرياضيات الكلاسيكية ، الهندسة التحليلية ، والمعروفة أيضًا باسم هندسة الإحداثيات أو الهندسة الديكارتية ، هي دراسة الهندسة باستخدام نظام إحداثيات. هذا يتناقض مع الهندسة التركيبية.
الهندسة الجبرية والهندسة التحليلية: في الرياضيات ، تعتبر الهندسة الجبرية والهندسة التحليلية موضوعين وثيقين الصلة. بينما تدرس الهندسة الجبرية الأصناف الجبرية ، تتعامل الهندسة التحليلية مع المشعبات المعقدة والمساحات التحليلية الأكثر عمومية المحددة محليًا من خلال تلاشي الوظائف التحليلية للعديد من المتغيرات المعقدة. للعلاقة العميقة بين هذه الموضوعات العديد من التطبيقات التي يتم فيها تطبيق التقنيات الجبرية على المساحات التحليلية والتقنيات التحليلية للأصناف الجبرية.
القواعد الرسمية: في نظرية اللغة الرسمية ، تصف القواعد كيفية تكوين سلاسل من أبجدية اللغة تكون صالحة وفقًا لتركيب اللغة. لا تصف القواعد النحوية معنى السلاسل أو ما يمكن فعله بها في أي سياق - فقط شكلها. يتم تعريف القواعد الرسمية على أنها مجموعة من قواعد الإنتاج للسلاسل في لغة رسمية.
جرافون: في نظرية الرسم البياني والإحصاء ، يعد الجرافون دالة متماثلة قابلة للقياس ، هذا مهم في دراسة الرسوم البيانية الكثيفة. تنشأ الجرافونات كمفهوم طبيعي لحد تسلسل الرسوم البيانية الكثيفة ، وككائنات تعريف أساسية لنماذج الرسم البياني العشوائية القابلة للتبديل. ترتبط الجرافونات برسوم بيانية كثيفة من خلال زوج الملاحظات التالي: نماذج الرسم البياني العشوائية المحددة بواسطة الجرافونات تؤدي إلى رسوم بيانية كثيفة بشكل شبه مؤكد ، ومن خلال انتظام lemma ، تلتقط الجرافونات بنية الرسوم البيانية الكبيرة الكثيفة التعسفية.
مجموعة الكذب: في الرياضيات ، مجموعة لي هي مجموعة متنوعة قابلة للتفاضل أيضًا. متشعب هو الفضاء الذي يشبه محليًا الفضاء الإقليدي ، في حين أن المجموعات تحدد المفهوم العام المجرد للضرب وأخذ المقلوب (الانقسام). بدمج هاتين الفكرتين ، يحصل المرء على مجموعة متصلة حيث يمكن مضاعفة النقاط معًا ، ويمكن أخذ معكوسها. بالإضافة إلى ذلك ، إذا تم تعريف الضرب وأخذ المقلوبات على أنها سلسة (قابلة للتفاضل) ، يحصل المرء على مجموعة لاي.
التأويلات: التأويل هو نظرية ومنهجية التفسير ، وخاصة تفسير النصوص التوراتية ، وأدب الحكمة ، والنصوص الفلسفية. التأويلات هي أكثر من مجرد مبادئ أو طرق تفسيرية مستخدمة عند فشل الفهم الفوري وتتضمن فن الفهم والتواصل.
التسلسل الهرمي التحليلي: في المنطق الرياضي ونظرية المجموعة الوصفية ، يعد التسلسل الهرمي التحليلي امتدادًا للتسلسل الهرمي الحسابي. يتضمن التسلسل الهرمي التحليلي للصيغ الصيغ بلغة الحساب من الدرجة الثانية ، والتي يمكن أن تحتوي على محددات كمية على كل من مجموعة الأرقام الطبيعية ، ، وما يزيد عن وظائف من ل . التسلسل الهرمي التحليلي للمجموعات يصنف المجموعات بواسطة الصيغ التي يمكن استخدامها لتحديدها ؛ إنها نسخة lightface للتسلسل الهرمي الإسقاطي.
عملية التحليل الوراثي: عملية التسلسل الهرمي التحليلي ( AHP ) ، وهي أيضًا عملية التسلسل الهرمي التحليلي ، هي تقنية منظمة لتنظيم وتحليل القرارات المعقدة ، بناءً على الرياضيات وعلم النفس. تم تطويره بواسطة Thomas L. Saaty في السبعينيات ؛ دخلت Saaty في شراكة مع Ernest Forman لتطوير برنامج Expert Choice في عام 1983 ، وخضع برنامج AHP للدراسة والتنقيح على نطاق واسع منذ ذلك الحين. إنه يمثل نهجًا دقيقًا لتحديد أوزان معايير القرار. تُستخدم خبرات الخبراء الفرديين لتقدير المقادير النسبية للعوامل من خلال المقارنات الزوجية. يقارن كل من المستجيبين الأهمية النسبية لكل زوج من العناصر باستخدام استبيان مصمم خصيصًا.
عملية التسلسل الهرمي التحليلي - مثال على السيارة: هذا مثال عملي يوضح استخدام عملية التسلسل الهرمي التحليلي (AHP) في موقف قرار عملي.
عملية التسلسل الهرمي التحليلي - مثال القائد: هذا مثال عملي يوضح استخدام عملية التسلسل الهرمي التحليلي (AHP) في موقف قرار عملي.
عملية التسلسل الهرمي التحليلي - مثال على السيارة: هذا مثال عملي يوضح استخدام عملية التسلسل الهرمي التحليلي (AHP) في موقف قرار عملي.
عملية التسلسل الهرمي التحليلي - مثال القائد: هذا مثال عملي يوضح استخدام عملية التسلسل الهرمي التحليلي (AHP) في موقف قرار عملي.
عملية التسلسل الهرمي التحليلي - مثال على السيارة: هذا مثال عملي يوضح استخدام عملية التسلسل الهرمي التحليلي (AHP) في موقف قرار عملي.
عملية التسلسل الهرمي التحليلي - مثال القائد: هذا مثال عملي يوضح استخدام عملية التسلسل الهرمي التحليلي (AHP) في موقف قرار عملي.
الهندسة الزائدية: في الرياضيات ، الهندسة الزائدية هي هندسة غير إقليدية. يتم استبدال الفرضية المتوازية للهندسة الإقليدية بـ: بالنسبة لأي خط معين R ونقطة P ليست على R ، في المستوى الذي يحتوي على كل من الخط R والنقطة P ، يوجد على الأقل خطان متميزان عبر P لا يتقاطعان مع R.
عامل الضغط المنخفض: في نظرية المعادلات التفاضلية الجزئية ، عامل تفاضلي جزئي المعرفة في مجموعة فرعية مفتوحة
المثالية الموضوعية: المثالية الموضوعية هي ميتافيزيقية مثالية تفترض أنه لا يوجد سوى مدرك واحد في النهاية ، وأن هذا المدرك هو أيضًا ما يُدرك. في هذه المدرسة الفكرية ، تتحد الكائنات الفردية وتصوراتها المحلية من خلال اللاوعي الجماعي.
الحث التحليلي: الحث التحليلي هو استراتيجية بحثية في علم الاجتماع تهدف إلى تطوير التفسيرات السببية لأنواع الظواهر بشكل منهجي. تم تحديده لأول مرة بواسطة فلوريان زانيكي في عام 1934. وقارنه بنوع من خاصية الاستقراء العددي المميزة للتحليل الإحصائي. حيث كان الأخير راضٍ عن الارتباطات الاحتمالية ، أصر زنانيكي على أن العلم يهتم باكتشاف المسلمات السببية ، وأن الاستقراء التحليلي في العلوم الاجتماعية هو وسيلة لاكتشافها.
الصحافة التحليلية: الصحافة التحليلية هي مجال من مجالات الصحافة التي تسعى إلى فهم الواقع المعقد من أجل خلق فهم عام. فهو يجمع بين جوانب الصحافة الاستقصائية والتقارير التفسيرية. يمكن النظر إلى الصحافة التحليلية على أنها استجابة للتواصل الاحترافي من العملاء الأقوياء ، والحمل الزائد للمعلومات ، والتعقيد المتزايد في عالم تسوده العولمة. ويهدف إلى إنشاء تفسيرات تستند إلى الأدلة للواقع ، وغالبًا ما تواجه طرقًا مهيمنة لفهم ظاهرة معينة.
المنطق التحليلي: يشير التفكير التحليلي إلى القدرة على النظر إلى المعلومات ، سواء كانت نوعية أو كمية بطبيعتها ، وتمييز الأنماط داخل المعلومات. يتضمن التفكير التحليلي التفكير الاستنتاجي بدون معرفة متخصصة ، مثل: فهم البنية الأساسية لمجموعة من العلاقات ؛ التعرف على العبارات المكافئة منطقيًا ؛ واستنتاج ما يمكن أن يكون صحيحًا أو يجب أن يكون صحيحًا من حقائق وقواعد معينة. التفكير التحليلي بديهي من حيث أن حقيقته بديهية. في المقابل ، يتطلب التفكير التركيبي تضمين الملاحظات التجريبية ، والتي دائمًا ما تكون عرضة للشك. تم تقديم المصطلحات المحددة "التحليلية" و "التركيبية" نفسها بواسطة كانط (1781) في بداية كتابه " نقد العقل الصافي" .
الفقه التحليلي: الفقه التحليلي هو نهج فلسفي للقانون يعتمد على موارد الفلسفة التحليلية الحديثة لمحاولة فهم طبيعتها. نظرًا لأن حدود الفلسفة التحليلية غامضة نوعًا ما ، فمن الصعب تحديد مدى امتدادها. ربما كان HLA Hart هو الكاتب الأكثر تأثيراً في مدرسة الفقه التحليلي الحديثة ، على الرغم من أن تاريخها يعود على الأقل إلى جيريمي بينثام.
التمييز التحليلي التركيبي: التمييز التحليلي التركيبي هو تمييز دلالي ، يستخدم بشكل أساسي في الفلسفة للتمييز بين الافتراضات التي تتكون من نوعين: الافتراضات التحليلية والافتراضات التركيبية . تكون الافتراضات التحليلية صحيحة أو غير صحيحة فقط بحكم معناها ، في حين أن حقيقة الافتراضات التركيبية ، إن وجدت ، مشتقة من كيفية ارتباط معناها بالعالم.
لغة تحليلية: في التصنيف اللغوي ، اللغة التحليلية هي لغة تنقل العلاقات بين الكلمات في الجمل بشكل أساسي عن طريق الكلمات المساعدة وترتيب الكلمات ، بدلاً من استخدام التصريفات. على سبيل المثال ، العبارة الإنجليزية "القطة تطارد الكرة" تنقل حقيقة أن القطة تعمل على الكرة بشكل تحليلي عبر ترتيب الكلمات. يمكن أن يتناقض هذا مع اللغات التركيبية ، التي تعتمد بشكل كبير على التصريفات لنقل العلاقات بين الكلمات. معظم اللغات ليست تحليلية بحتة ، لكن العديد منها يعتمد بشكل أساسي على التركيب التحليلي.
لغة تحليلية: في التصنيف اللغوي ، اللغة التحليلية هي لغة تنقل العلاقات بين الكلمات في الجمل بشكل أساسي عن طريق الكلمات المساعدة وترتيب الكلمات ، بدلاً من استخدام التصريفات. على سبيل المثال ، العبارة الإنجليزية "القطة تطارد الكرة" تنقل حقيقة أن القطة تعمل على الكرة بشكل تحليلي عبر ترتيب الكلمات. يمكن أن يتناقض هذا مع اللغات التركيبية ، التي تعتمد بشكل كبير على التصريفات لنقل العلاقات بين الكلمات. معظم اللغات ليست تحليلية بحتة ، لكن العديد منها يعتمد بشكل أساسي على التركيب التحليلي.
مشعب تحليلي: في الرياضيات ، يوجد متشعب تحليلي ، يُعرف أيضًا باسم أ متشعب ، هو مشعب قابل للتفاضل مع خرائط انتقال تحليلية. يشير المصطلح عادة إلى المشعبات التحليلية الحقيقية ، على الرغم من أن المشعبات المعقدة هي أيضًا تحليلية. في الهندسة الجبرية ، تعتبر الفراغات التحليلية تعميمًا للمشعبات التحليلية بحيث يُسمح بالتفردات.
الوظيفة التحليلية: في الرياضيات ، الوظيفة التحليلية هي وظيفة تُعطى محليًا بواسطة سلسلة قوى متقاربة. توجد وظائف تحليلية حقيقية ووظائف تحليلية معقدة . وظائف كل نوع قابلة للتفاضل إلى ما لا نهاية ، ولكن الوظائف التحليلية المعقدة تظهر خصائص لا تنطبق بشكل عام على الوظائف التحليلية الحقيقية. تكون الوظيفة تحليلية فقط إذا كانت سلسلة Taylor الخاصة بها حول x 0 تتقارب مع الوظيفة في بعض الجوار لكل x 0 في مجالها.
الوظيفة التحليلية: في الرياضيات ، الوظيفة التحليلية هي وظيفة تُعطى محليًا بواسطة سلسلة قوى متقاربة. توجد وظائف تحليلية حقيقية ووظائف تحليلية معقدة . وظائف كل نوع قابلة للتفاضل إلى ما لا نهاية ، ولكن الوظائف التحليلية المعقدة تظهر خصائص لا تنطبق بشكل عام على الوظائف التحليلية الحقيقية. تكون الوظيفة تحليلية فقط إذا كانت سلسلة Taylor الخاصة بها حول x 0 تتقارب مع الوظيفة في بعض الجوار لكل x 0 في مجالها.